初一第一

一般，最后一题没打好

不难发现，教练出水了，可能是信心赛

A.不幸的7

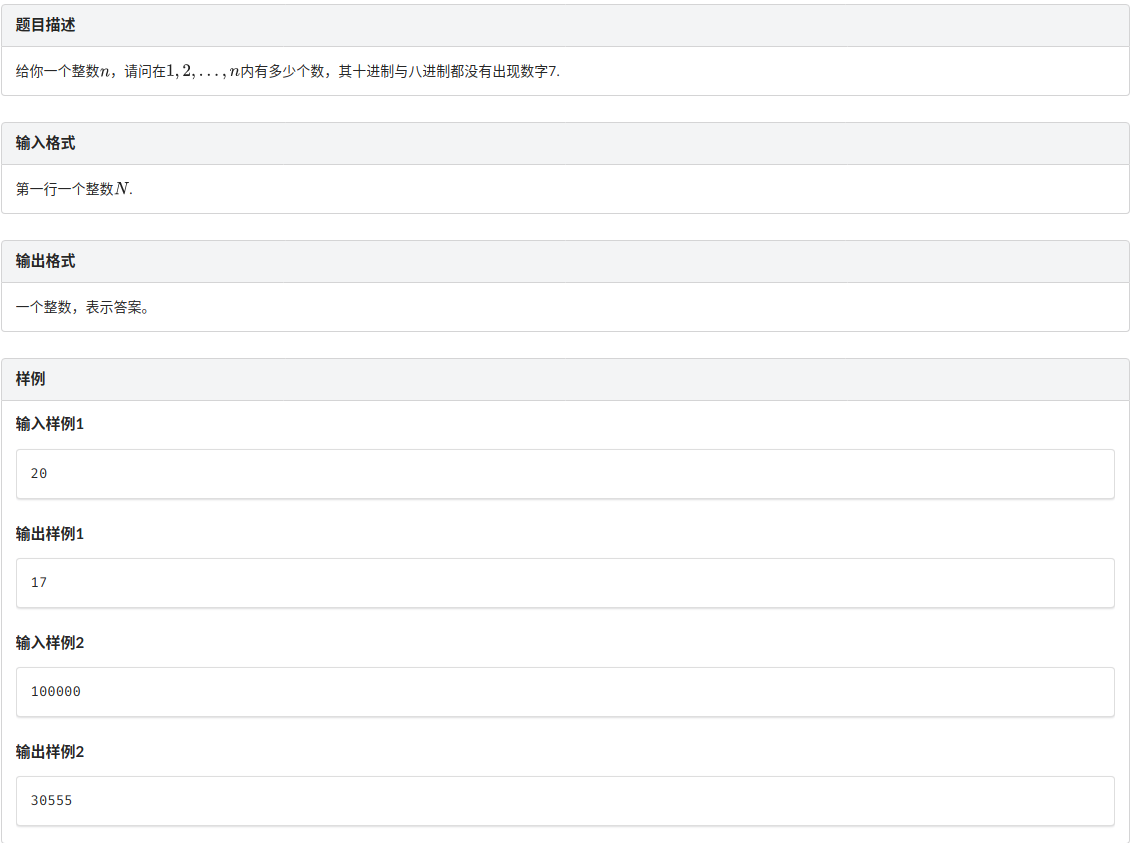
暴力，没有逻辑可言

#include<bits/stdc++.h>
using namespace std;
int n,ans,t,k;
bool pd(int x)
{
    while(x)
    {
        if(x%10==7)return false;
        x/=10;
    }
    return true;
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        k=i,t=0;
        while(k)
        {
            t*=10;
            t+=k%8;
            k/=8;
        }
        if(pd(i)&&pd(t))ans++;
    }
    cout<<ans;
}

B.选举

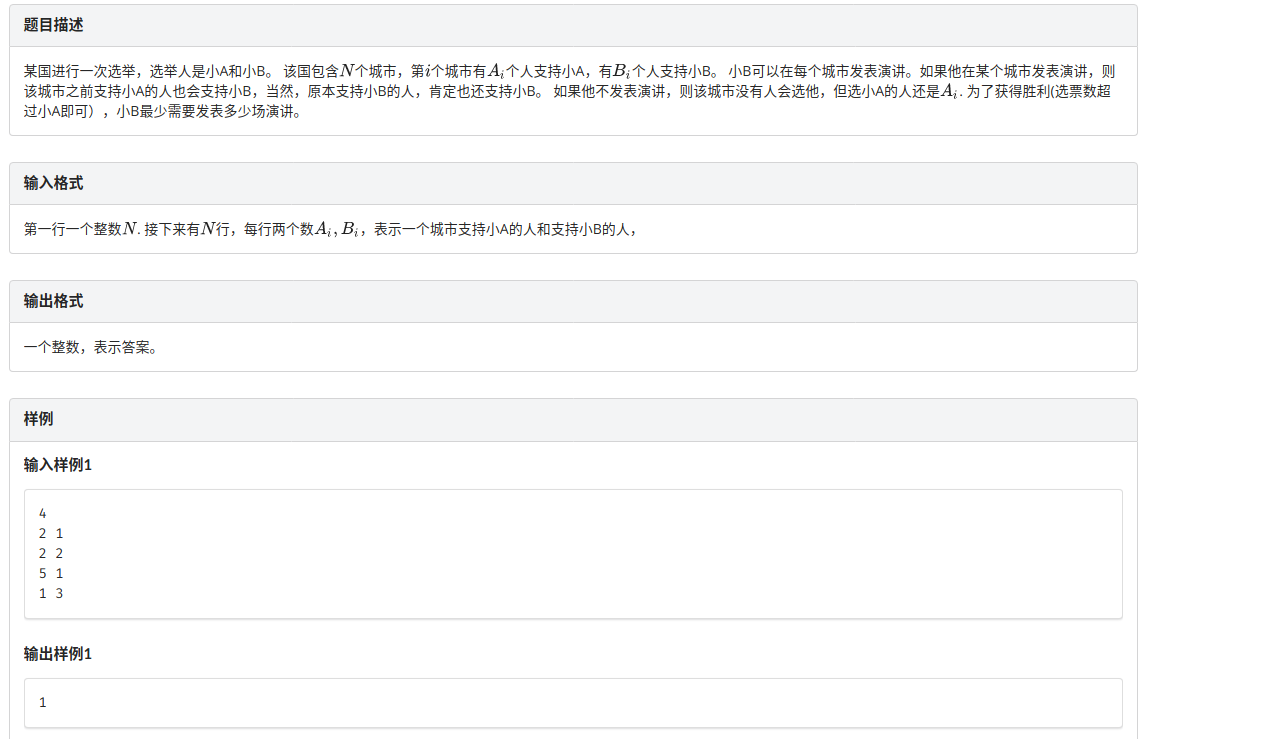
简单的贪心，思路很水，五分钟想出来

先固定A，问题变成让B追上A

A和B的初始的距离是什么？

$sumA=\sum_{i=1}^{n}a_i$

如果B什么都不做，A可以获得所有A支持者的选票

那一个城市能缩小多少距离呢

$w_i=b_i+2a_i$

首先，去一个城市，B的支持者和A的支持者都支持B，就是$b_i+a_i$,

A少了$a_i$个支持者，也加上去，就这样

#include<bits/stdc++.h>
using namespace std;
struct node
{
    long long a,b;
}a[1000005];
long long n,suma,k;
bool cmp(node x,node y)
{
    return x.a*2+x.b>y.a*2+y.b;
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        scanf("%lld%lld",&a[i].a,&a[i].b);
        suma+=a[i].a;
    }
    sort(a+1,a+n+1,cmp);
    while(suma>=0)
    {
        k++;
        suma-=a[k].a*2+a[k].b;
    }
    cout<<k;
}

C. 差的绝对值之和

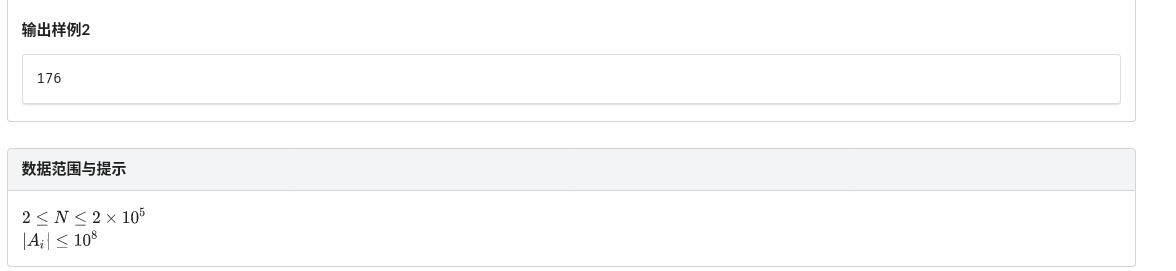
这道题水炸了，好好想，很有意思，不要直接看题解！

#include <bits/stdc++.h>
using namespace std;
long long n, a[1000005], sum, ans;
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    sort(a + 1, a + n + 1);
    sum = a[n];
    for (int i = n - 1; i >= 1; i--) {
        ans += sum - a[i] * (n - i);
        sum += a[i];
    }
    cout << ans;
}

D. 路径通过

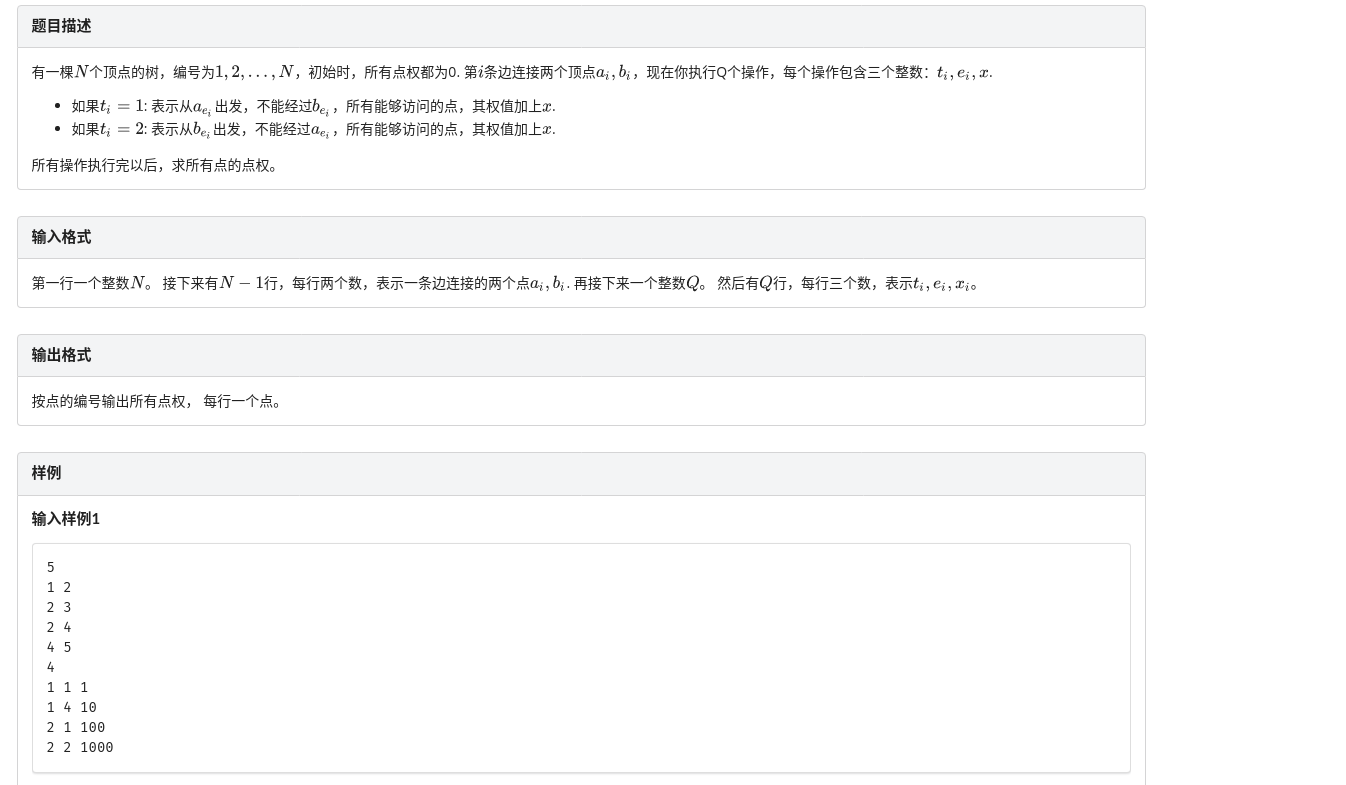
整体操作，先明确父子关系，然后对于每个操作，理解为对整个树和子树的操作，

最后的dfs统计即可

#include<bits/stdc++.h>
using namespace std;
struct node
{
    int t,next;
}a[500005];
long long n,m,x,y,z,tot,h[500005],fa[500005],s[500005],t[500005],w[500005],ans[500005];
void add(int x,int y)
{
    tot++;
    a[tot].t=y;
    a[tot].next=h[x];
    h[x]=tot;
}
void dfa(int x,int f)
{
    for(int i=h[x];i;i=a[i].next)
    {
        if(a[i].t!=f)
        {
            fa[a[i].t]=x;
            dfa(a[i].t,x);
        }
    }
}
void dfs(int x,int f)
{
    ans[x]=ans[f]+w[x];
    for(int i=h[x];i;i=a[i].next)
    {
        if(a[i].t!=f)
        {
            
            dfs(a[i].t,x);
        }
    }
}
int main()
{
    cin>>n;
    for(int i=1;i<=n-1;i++)
    {
        cin>>x>>y;
        add(x,y);
        add(y,x);
        s[i]=x;
        t[i]=y;
    }
    dfa(1,0);
    cin>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>x>>y>>z;
        if(x==1)
        {
            if(fa[t[y]]==s[y])
            {
                w[1]+=z;
                w[t[y]]-=z;
            }
            else
            {
                w[s[y]]+=z;
            }
        }
        else
        {
            if(fa[t[y]]==s[y])
            {
                w[t[y]]+=z;
            }
            else
            {
                w[1]+=z;
                w[s[y]]-=z;
            }
        }
    }
    dfs(1,0);
    for(int i=1;i<=n;i++)
    {
        cout<<ans[i]<<endl;
    }
}

按dfs序，变成一个数组，然后树状数组整体操作

E. 龙椅

这就是个Exgcd，我打出来真是万幸，就是找正整数解那段忘了，自己的又臭又长

$s+1+xk \equiv 1(mod\ n)$

x为题目所求
化简得

$xk-yn=-s$

求即可

#include<bits/stdc++.h>
using namespace std;
long long t,a,b,c,x,y,gcd;
void exgcd(long long a,long long b,long long &x,long long &y)
{
    if(!b)
    {
     //   cout<<a<<' '<<b<<endl;
        gcd=a;
        x=1;
        y=0;
        return;
    }
    
    exgcd(b,a%b,y,x);
    //cout<<a<<' '<<b<<' '<<x<<' '<<y<<endl;
    y-=((a/b)*x);
    
}
int main()
{
    cin>>t;
    for(int i=1;i<=t;i++)
    {
        cin>>b>>c>>a;
        x=0,y=0;
        exgcd(a,-b,x,y);
        
        if((-c)%gcd!=0)
        {
            cout<<-1<<endl;
            continue;
        }
        x*=-c/gcd;
        y*=-c/gcd;
        if((a*-b)/gcd>0)
        {
            y-=(a*-b)/gcd/b*(x/(a*-b)/gcd/a);
            x%=(a*-b)/gcd/a;
            while(x<0)
            {
                x+=(a*-b)/gcd/a;
                y-=(a*-b)/gcd/b;
            }
            y+=(a*-b)/gcd/b*(x/(a*-b)/gcd/a);
            x%=(a*-b)/gcd/a;
            while(x-((a*-b)/gcd)/a>=0)
            {
                x-=(a*-b)/gcd/a;
                y+=(a*-b)/gcd/b;
            }
        }
        else
        {
            y+=(a*-b)/gcd/b*(x/(a*-b)/gcd/a);
            x%=(a*-b)/gcd/a;
            while(x<0)
            {
                x-=(a*-b)/gcd/a;
                y+=(a*-b)/gcd/b;
            }
            y-=(a*-b)/gcd/b*(x/(a*-b)/gcd/a);
            x%=(a*-b)/gcd/a;
            while(x+((a*-b)/gcd)/a>=0)
            {
                x+=(a*-b)/gcd/a;
                y-=(a*-b)/gcd/b;
            }
        }
        cout<<x<<endl;
    }
}

第六题待做